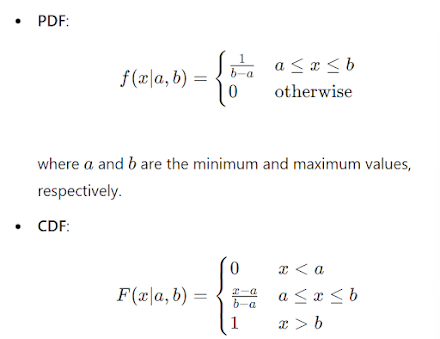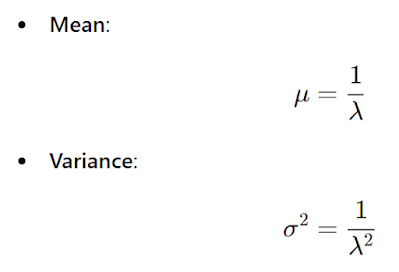Statistics for Data Science

Statistics

It is the science of gathering, describing, and analyzing data. The goal of statistics is to make better decision in our daily life using mathematics.

Branches of Statistics:

1. Descriptive Statistics

Descriptive statistics summarize and describe the features of a data set. Here are the key components:

• Measures of Central Tendency: These indicate the center of the data. Common measures are:

• Mean
• Median
• Mode

• Measures of Dispersion: These show how spread out the data points are. Common measures include:

• Range
• Variance
• Standard Deviation

• Graphs and Charts: Visual tools like bar charts, histograms, and pie charts to represent data visually.

2. Inferential Statistics

Inferential statistics make predictions or inferences about a population based on a sample of data. Key components include:

• Sampling: Selecting a representative group from the population to study.

• Random Sampling: Each member of the population has an equal chance of being selected.
• Stratified Sampling: The population is divided into subgroups, and samples are taken from each group.

• Hypothesis Testing: A method to test assumptions or claims about a population.
• Confidence Intervals: A range of values that estimate a population parameter with a certain level of confidence (e.g., 95% confidence interval).

Data Types

Categorical Data:

Categorical data represents categories or characteristics like gender, language, or movie genre. It's also called qualitative data. You can use numbers for them, but those numbers have no real math value (like 0/1 for male/female).

Types:

Nominal Data:

• No order.
• Examples: gender, language, eye color.
• Analyze with frequencies, pie charts, etc.

Ordinal Data:

• Has order.
• Examples: happiness level, education level, movie ratings.
• Summarize with median, mean, visualize with bar charts.

Binary Data:

• Just two values: yes or no.
• Represented as "True" and "False" or 1 and 0.

Numerical Data:

Numerical data is expressed as numbers, allowing quantification. It represents values like integers or real numbers. It is also called quantitative data. Examples include a person's height, product prices, IQ scores, the number of lessons in a course, etc.

Types:

1. Discrete Data

• Has a finite or countably infinite set of values.
• Values are distinct and separate.
• Examples: zip codes, words in a document collection, number of coin toss heads, students in a classroom, cars in a showroom.
• Often represented as integer variables.
• Analyzed using mean, median, quartiles, box plots, and histograms.

2. Continuous Data

• Cannot be counted but can be measured.
• Represents measurements.
• Examples: market share price, height/weight of a person, amount of rainfall, car speed, Wi-Fi frequency.
• Can be divided into meaningful parts.
• Has real numbers as attribute values.

Types of Continuous Data:

a. Interval Data

• Categorized, ranked, and evenly spaced.
• Values have order and can be positive, zero, or negative.
• Allows comparison and quantification of differences.
• Examples: temperatures in Celsius or Fahrenheit, calendar dates.

b. Ratio Data

• Numeric attribute with an inherent zero-point.
• Values can be multiples or ratios of one another.
• Ordered values with computed differences.
• Examples: Kelvin temperature scale, years of experience, number of words.

Measures of Central Tendency

Mean:

The mean is often referred to as the average. It's calculated by adding up all the values in a dataset and then dividing by the number of data points. Here's the advantage and limitation of using the mean:

Advantage of the Mean:

• The mean can be used for both continuous and discrete numeric data.

Limitations of the Mean:

• The mean cannot be calculated for categorical data because the values cannot be summed.
• The mean is not robust against outliers, meaning that a single large value (an outlier) can significantly skew the average.

import pandas as pd

# Create a DataFrame
data = {'Name': ['Alice', 'Bob', 'Charlie'],
        'Age': [25, 30, 35],
        'Salary': [70000, 80000, 90000]}
df = pd.DataFrame(data)

# Mean of the Age and Salary columns
print(df[['Age', 'Salary']].mean())

# Output:
# Age          30.0
# Salary    80000.0
# dtype: float64

Median:

The median is the middle value in a dataset when it's ordered from smallest to largest. The median is less affected by outliers and skewed data, making it a preferred measure of central tendency when the data distribution is not symmetrical.

2 2 5 6 7 8 9

# Median of the Age and Salary columns
print(df[['Age', 'Salary']].median())

# Output:
# Age          30.0
# Salary    80000.0
# dtype: float64

Mode:

The mode is the value that occurs most frequently in a dataset.

2 2 5 6 7 8 9

Advantage of the Mode:

• Unlike the mean and median, which are mainly used for numeric data, the mode can be found for both numerical and categorical (non-numeric) data.

Limitation of the Mode:

• In some distributions, the mode may not reflect the center of the distribution very well, especially if the data is multimodal (has multiple modes) or if all values occur with similar frequencies.

import pandas as pd

# Create a DataFrame
data = {'Name': ['Alice', 'Bob', 'Charlie', 'Julia'],
        'Age': [25, 30, 35, 25],
        'Salary': [70000, 80000, 90000, 40000]}
df = pd.DataFrame(data)

# Mode of the Age column
print(df['Age'].mode())

# Output:
# 0    25
# Name: Age, dtype: int64

Measure of Position

Quantile:

Quantiles are values that divide a dataset into equal-sized intervals. For instance, the 0.5 quantile is the median, which divides the data into two equal halves. Commonly used quantiles include:

Quartiles: Divides the data into four equal parts.

• Q1 (First Quartile): 25th percentile.
• Q2 (Second Quartile/Median): 50th percentile.
• Q3 (Third Quartile): 75th percentile.

import pandas as pd

# Sample data
data = {
    'values': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
}
df = pd.DataFrame(data)

# Calculate quantiles
Q1 = df['values'].quantile(0.25)
Q2 = df['values'].quantile(0.50)
Q3 = df['values'].quantile(0.75)

print(f"First Quartile (Q1): {Q1}")
print(f"Second Quartile (Q2/Median): {Q2}")
print(f"Third Quartile (Q3): {Q3}")

# Output:
# First Quartile (Q1): 32.5
# Second Quartile (Q2/Median): 55.0
# Third Quartile (Q3): 77.5

Measures of Dispersion

Measures of dispersion provide insights into how data values are spread out or vary within a dataset. Common measures of dispersion include the range, variance, standard deviation.

Range:

The range is the simplest measure of dispersion. It's calculated by subtracting the minimum value from the maximum value in the dataset. While it's easy to compute, it's sensitive to extreme values (outliers) and may not provide a complete picture of data variability.

import pandas as pd

# Create a DataFrame
data = {'Name': ['Alice', 'Bob', 'Charlie', 'Julia'],
        'Age': [25, 30, 35, 25],
        'Salary': [70000, 80000, 90000, 40000]}
df = pd.DataFrame(data)

# Range of the Age column
print(df['Age'].max() - df['Age'].min())

# Output:
# 10

Interquartile Range (IQR):

The Interquartile Range (IQR) is a measure of statistical dispersion. It is calculated as the difference between the third quartile (Q3) and the first quartile (Q1):

IQR = Q3 − Q1

The IQR represents the middle 50% of the data and is useful for identifying outliers.

import pandas as pd

# Sample data
data = {
    'values': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
}
df = pd.DataFrame(data)

# Calculate quantiles
Q1 = df['values'].quantile(0.25)
Q3 = df['values'].quantile(0.75)

# Calculate IQR
IQR = Q3 - Q1

print(f"Interquartile Range (IQR): {IQR}")

# Output the results
# Interquartile Range (IQR): 45.0

Variance and Standard Deviation:

Variance is a measure that quantifies how far each data point is from the mean.

Standard deviation is the square root of the variance and provides a measure of dispersion in the same units as the data.

These measures give us a more detailed understanding of how data points deviate from the mean. Higher variance and standard deviation values indicate greater data spread.

import pandas as pd

# Create a DataFrame
data = {'Name': ['Alice', 'Bob', 'Charlie', 'Julia'],
        'Age': [25, 30, 35, 25],
        'Salary': [70000, 80000, 90000, 40000]}
df = pd.DataFrame(data)

# Variance of the Age column
print(df['Age'].var())

# Output:
# 22.916666666666668

# Standard deviation of the Age column
print(df['Age'].std())

# Output:
# 4.7871355387816905

Five-Number Summary:

The five-number summary provides a quick overview of a dataset's distribution. It includes:

• Minimum: The smallest data point.
• First Quartile (Q1): The 25th percentile, where 25% of the data points are below this value.
• Median (Q2): The 50th percentile, the middle value that divides the dataset into two equal parts.
• Third Quartile (Q3): The 75th percentile, where 75% of the data points are below this value.
• Maximum: The largest data point.

Boxplot:

A boxplot is a graphical representation of the five-number summary. It visually shows the distribution of data through their quartiles. The "box" represents the interquartile range (IQR), and "whiskers" extend to the minimum and maximum values, excluding outliers. Outliers are shown as individual points.

Basically, sometimes, you may have data points that are far from the rest of your data. These are considered as outliers. To check outliers, you have to find the lower and upper bounds based on IQR.

Lower Bound = Q1 - 1.5 (IQR)

Upper Bound = Q3 + 1.5 (IQR)

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Sample data with potential outliers
data = {
    'values': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200]
}
df = pd.DataFrame(data)

# Calculate the five-number summary
minimum = df['values'].min()
Q1 = df['values'].quantile(0.25)
median = df['values'].median()
Q3 = df['values'].quantile(0.75)
maximum = df['values'].max()
IQR = Q3 - Q1

# Determine outliers
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = df[(df['values'] < lower_bound) | (df['values'] > upper_bound)]

# Output the five-number summary and outliers
print(f"Minimum: {minimum}")
print(f"First Quartile (Q1): {Q1}")
print(f"Median (Q2): {median}")
print(f"Third Quartile (Q3): {Q3}")
print(f"Maximum: {maximum}")
print(f"IQR: {IQR}")
print(f"Lower Bound for Outliers: {lower_bound}")
print(f"Upper Bound for Outliers: {upper_bound}")
print("Outliers:")
print(outliers)

# Minimum: 10
# First Quartile (Q1): 35.0
# Median (Q2): 60.0
# Third Quartile (Q3): 85.0
# Maximum: 200
# IQR: 50.0
# Lower Bound for Outliers: -40.0
# Upper Bound for Outliers: 160.0
# Outliers:
#     values
# 10     200

# Draw a boxplot
sns.boxplot(x=df['values'])
plt.title('Boxplot of Values with Outliers')
plt.xlabel('Values')
plt.show()

Measuring Chance

Probability deals with the uncertainty and randomness. It provides a way to quantify the likelihood or chance of events occurring.

• The probability of an event to occur is b/w 0 & 1.
• 0 indicates impossibility of event.
• 1 indicates certainty of event.

P(E) = Number of Favorable Outcomes / Total number of Outcomes

Example: A coin flip.

P(Heads) = 1 way to get heads / 2 possible outcomes = 1 / 2 = 0.50 = 50%

So, there are 50% chances to get a head.

Independent Events:

Two events are independent if the occurrence of one event does not affect the probability of the other event occurring.

Example: Sampling with replacement - Each pick is independent.

In this scenario, each item is returned to the population after being picked, keeping the probabilities of subsequent picks unaffected.

• First Pick: There are four options (Amir, Brian, Claire, Damian).
• Second Pick: After one item is picked, it is replaced, leaving four options again.

import numpy as np
import pandas as pd

# Set the random seed for reproducibility
np.random.seed(42)

# Define a population
data = {"Column1" : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}
population = pd.DataFrame(data)

# Sample 5 items with replacement
sample_with_replacement = population.sample(5, replace=True)
print("Sample with Replacement:\n", sample_with_replacement)

# Output:
# Sample with Replacement:
#     Column1
# 6        7
# 3        4
# 7        8
# 4        5
# 6        7

Dependent Events:

Two events are dependent if the occurrence of one event affects the probability of the other event occurring.

Example: Sampling without replacement - Each pick is dependent.

In this scenario, each item is not returned to the population after being picked, affecting the probabilities of subsequent picks.

• First Pick: There are four options (Amir, Brian, Damian, Claire).
• Second Pick: After one item is picked, it is not replaced, leaving three options.

import numpy as np

# Set the random seed for reproducibility
np.random.seed(42)

# Define a population
data = {"Column1" : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}
population = pd.DataFrame(data)

# Sample 5 items without replacement
sample_without_replacement = population.sample(5, replace=False)
print("Sample without Replacement:\n", sample_without_replacement)

# Output:
# Sample without Replacement:
#     Column1
# 8        9
# 1        2
# 5        6
# 0        1
# 7        8

Discrete Distribution

A discrete distribution describes the probability distribution of a discrete random variable. A discrete random variable is one that can take on a countable number of distinct values. The probability distribution provides the probability of each possible value.

Characteristics:

• Countable Outcomes: The values that the random variable can take are distinct and countable (e.g., integers).
• Probability Mass Function (PMF): This function gives the probability that a discrete random variable is exactly equal to some value.
• Sum of Probabilities: The sum of all probabilities for all possible values is equal to 1.
• Cumulative Distribution Function (CDF): This function gives the probability that the random variable is less than or equal to some value.

Binomial Distribution:

Models the number of successes in a fixed number of independent Bernoulli trials. The PMF is:

Example:

from scipy import stats

# What's the probability of 7 heads? P(heads = 7)

print(stats.binom.pmf(k = 7, n = 10, p = 0.5))

# 0.11718749999999999

# What's the probability of 7 or fewer heads? P(heads <= 7)

print(stats.binom.cdf(k = 7, n = 10, p = 0.5))

# 0.9453125

# What's the probability of more than 7 heads? P(heads > 7)

print(1 - stats.binom.cdf(k = 7, n = 10, p = 0.5))

# 0.0546875

Poisson Distribution:

Models the number of times an event occurs in a fixed interval of time or space.

Examples:

• Number of animals adopted from an animal shelter per week
• Number of people arriving at a restaurant per hour

from scipy import stats

# If the average number of adoptions per week is 8, what is P(X=5)

print(stats.poisson.pmf(k = 5, mu = 8))

# 0.09160366159257921

# If the average number of adoptions per week is 8, what is P(X≤5)

print(stats.poisson.cdf(k = 5, mu = 8))

# 0.19123606207962532

# If the average number of adoptions per week is 8, what is P(X>5)

print(1 - stats.poisson.cdf(k = 5, mu = 8))

# 0.8087639379203747

Continuous Distribution

A continuous distribution describes the probability distribution of a continuous random variable. A continuous random variable can take on an infinite number of possible values within a given range. The probability of the variable taking on an exact value is zero; instead, probabilities are given for ranges of values.

Characteristics:

• Uncountable Outcomes: The values that the random variable can take are not countable (e.g., real numbers).
• Probability Density Function (PDF): This function gives the probability that a continuous random variable falls within a particular range of values.
• Total Area Under the Curve: The area under the PDF curve is equal to 1.
• Cumulative Distribution Function (CDF): This function gives the probability that a continuous random variable is less than or equal to a certain value. It is the integral of the PDF.

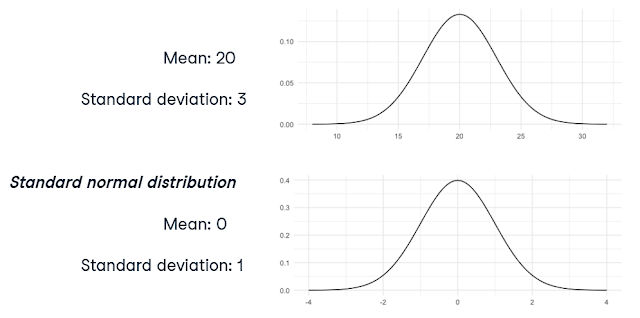
Normal Distribution:

The normal distribution, also known as the Gaussian distribution, is one of the most important continuous distributions. It is characterized by its bell-shaped curve, symmetric about the mean.

Properties:

• Symmetric about the mean.
• Mean, median, and mode are all equal.
• The total area under the curve is 1.

from scipy.stats import norm

# If mean is 161 cm and standard deviation is 7 cm then what percent of women are shorter than 154 cm

norm.cdf(154, 161, 7)

# 0.158655

# What percent of women are taller than 154 cm

1 - norm.cdf(154, 161, 7)

# 0.841345

# What percent of women are 154-157 cm

norm.cdf(157, 161, 7) - norm.cdf(154, 161, 7)

# 0.1252

Uniform Distribution:

The uniform distribution is a continuous distribution that has constant probability over a given range. It is the simplest type of continuous distribution.

Properties:

• All intervals of the same length are equally probable.
• The total area under the curve is 1.

from scipy.stats import uniform

# P(X≤7)

uniform.cdf(7, 0, 12)

# 0.5833333

Exponential Distribution:

The exponential distribution is used to model the time between events in a Poisson process, where events occur continuously and independently at a constant average rate.

from scipy.stats import expon

# P(X<1)

expon.cdf(1, scale=2)

# 0.3934693402873666

# P(X>4)

1 - expon.cdf(4, scale=2)

# 0.1353352832366127

# P(1<X<4)

expon.cdf(4, scale=2) - expon.cdf(1, scale=2)

# 0.4711953764760207

The Central Limit Theorem

The Central Limit Theorem (CLT) is a fundamental concept in statistics that describes how the distribution of sample means approaches a normal distribution as the sample size increases, regardless of the distribution of the original population. This theorem is essential because it allows statisticians to make inferences about population parameters using sample data.

Key Points of the Central Limit Theorem:

• Sampling Distribution: The distribution of a statistic (like the mean) calculated from multiple samples of a given size.
• Normal Distribution: As the sample size increases, the sampling distribution of the sample mean will approach a normal distribution.
• Independence: Samples should be random and independent of each other.
• Large Sample Size: Typically, a sample size of 30 or more is considered sufficient for the CLT to hold, although this can vary depending on the population distribution.

Example: Rolling a Die

Let's illustrate the Central Limit Theorem using a simple example of rolling a six-sided die multiple times.

Rolling the Die 5 Times:

import pandas as pd
import numpy as np

# Create a series representing a six-sided die
die = pd.Series([1, 2, 3, 4, 5, 6])

# Roll the die 5 times with replacement
samp_5 = die.sample(5, replace=True)
print(samp_5.values)
np.mean(samp_5)

Output might be:

array([3, 1, 4, 1, 1])
2.0

Rolling the Die 5 Times, 10 Times:

Repeat the process 10 times and store the sample means.

sample_means = []
for i in range(10):
    samp_5 = die.sample(5, replace=True)
    sample_means.append(np.mean(samp_5))

print(sample_means)

Output might be:

[3.8, 4.0, 3.8, 3.6, 3.2, 4.8, 2.6, 3.0, 2.6, 2.0]

The Central Limit Theorem states that the sampling distribution of a statistic becomes closer to the normal distribution as the number of trials increases.

import matplotlib.pyplot as plt
import seaborn as sns

# Generate 1000 sample means
sample_means = [np.mean(die.sample(5, replace=True)) for _ in range(1000)]

# Plot the distribution of sample means
sns.histplot(sample_means)
plt.title('Sampling Distribution of the Sample Mean')
plt.xlabel('Sample Mean')
plt.ylabel('Frequency')
plt.show()

Sampling Methods

Sampling is the process of selecting a subset of individuals or items from a larger population to estimate characteristics of the whole population. There are various sampling methods, each with its own advantages and applications. Here, we will discuss three common types: Simple Random Sampling, Systematic Sampling, and Stratified Random Sampling.

1. Simple Random Sampling:

Definition: Simple random sampling is a basic sampling technique where each member of the population has an equal chance of being selected.

Example:

import pandas as pd

# Create a DataFrame representing a population of 100 people/items
population = pd.DataFrame({'id': range(1, 101)})

# Select a random sample of 10
sample_size = 10
simple_random_sample = population.sample(n=sample_size, replace=False, random_state=1)
print("Simple Random Sample:\n", simple_random_sample)

# Simple Random Sample:
#     id
# 80  81
# 84  85
# 33  34
# 81  82
# 93  94
# 17  18
# 36  37
# 82  83
# 69  70
# 65  66

2. Systematic Sampling:

Definition: Systematic sampling involves selecting members of the population at regular intervals.

Example:

import pandas as pd

# Create a DataFrame representing a population of 100 people/items
population = pd.DataFrame({'id': range(1, 101)})

# Define the sample size
sample_size = 10
interval = len(population) // sample_size  # Sampling interval

# Select a random starting point between 0 and k-1
systematic_sample = population.iloc[::interval]

print("Systematic Sample:\n", systematic_sample)

# Systematic Sample:
#     id
# 0    1
# 10  11
# 20  21
# 30  31
# 40  41
# 50  51
# 60  61
# 70  71
# 80  81
# 90  91

3. Stratified Random Sampling:

Definition: Stratified random sampling involves dividing the population into distinct subgroups and then taking a random sample from each subgroup.

Example:

import pandas as pd

# Example dataset (to be replaced with actual data)
coffee_ratings = pd.DataFrame({
    'country_of_origin': [
        'Mexico', 'Colombia', 'Guatemala', 'Brazil', 'Taiwan', 'United States (Hawaii)',
        'Mexico', 'Colombia', 'Guatemala', 'Brazil', 'Taiwan', 'United States (Hawaii)',
        # ... (more data)
    ]
})

# Define the top six countries
top_counted_countries = ["Mexico", "Colombia", "Guatemala", "Brazil", "Taiwan", "United States (Hawaii)"]

# Filter the dataset for the top six countries
top_counted_subset = coffee_ratings['country_of_origin'].isin(top_counted_countries)
coffee_ratings_top = coffee_ratings[top_counted_subset]

# Perform proportional stratified sampling
coffee_ratings_strat = coffee_ratings_top.groupby("country_of_origin").sample(frac=0.1, random_state=2021)

# Show the value counts
stratified_proportional_counts = coffee_ratings_strat['country_of_origin'].value_counts(normalize=True)
print("Proportional Stratified Sample Proportions:\n", stratified_proportional_counts)

# Proportional Stratified Sample Proportions:
# Mexico                    0.25
# Colombia                  0.18
# Guatemala                 0.17
# Brazil                    0.15
# United States (Hawaii)    0.14
# Taiwan                    0.11
# Name: country_of_origin, dtype: float64

# Perform equal counts stratified sampling
coffee_ratings_eq = coffee_ratings_top.groupby("country_of_origin").sample(n=15, random_state=2021)

# Show the value counts
stratified_equal_counts = coffee_ratings_eq['country_of_origin'].value_counts(normalize=True)
print("Equal Counts Stratified Sample Proportions:\n", stratified_equal_counts)

# Equal Counts Stratified Sample Proportions:
# Brazil                    0.167
# Colombia                  0.167
# Guatemala                 0.167
# Mexico                    0.167
# Taiwan                    0.167
# United States (Hawaii)    0.167
# Name: country_of_origin, dtype: float64

Hypothesis Testing

Hypothesis testing is a statistical method used to make inferences or draw conclusions about a population based on sample data. It involves formulating two competing hypotheses, the null hypothesis H_0 and the alternative hypothesis H_1, and then using sample data to determine which hypothesis is supported.

Steps in Hypothesis Testing:

1. State the hypotheses: Define the null and alternative hypotheses.

• Null Hypothesis (H_0): The statement being tested in a statistical test is called the null hypothesis, denoted by H_0. The test is designed to assess and determine the strength of evidence in the data against the null hypothesis H_0.
• Alternative Hypothesis (H_1): What you want to accept as true when you reject the null hypothesis.

One should reach out at one of the following conclusions:

• Reject H_0 in favor of H_1 because of sufficient evidence in the data.
• Fail to reject H_0 because of insufficient evidence in the data.

One-Tailed vs. Two-Tailed Tests

When performing hypothesis tests, the direction of the test is determined by the nature of the research question. This leads to either a one-tailed or a two-tailed test.

One-Tailed Test:

A one-tailed test is used when the research hypothesis specifies a direction of the effect or difference. There are two types of one-tailed tests:

1. Right-Tailed Test: Used when we are testing if a sample mean is greater than the population mean.

Hypotheses:

2. Left-Tailed Test: Used when we are testing if a sample mean is less than the population mean.

Hypotheses:

Two-Tailed Test:

A two-tailed test is used when the research hypothesis does not specify a direction of the effect or difference. It tests if the sample mean is simply different from the population mean.

Hypotheses:

2. Choose a significance level (alpha):

As, hypothesis test are based on sample information, we must allow for the possibility of errors. There are two types of errors that can be made in hypothesis testing:

• Type 1 Error: Rejecting the null hypothesis when it is true. It is denoted as alpha.
• Type 2 Error: Not rejecting the null hypothesis when it is false. It is denoted by beta.

The level of significance gives or represents the probability of making a Type 1 error, which is rejecting the null hypothesis when it is true. Common choices are 0.05, 0.01, and 0.10.

3. Collect data: Gather sample data.

4. Perform the test: Calculate the test statistic (e.g., Z-score).

One-Sample Z-Test

The Z-test is a statistical test used to determine whether there is a significant difference between the means of two groups. It is typically used when the sample size is large (usually n > 30) or when the population variance is known.

One-Sample Z-Test Formula:

One-Sample T-Test

The T-test is similar to the Z-test but is used when the population variance is unknown and the sample size is small. It uses the sample standard deviation instead of the population standard deviation.

One-Sample T-Test Formula:

5. Use Critical Region: The significance level helps specify the size of the region where the null hypothesis should be rejected. We call that region, the critical region.

For Two Tailed:

The critical region is in the two extreme regions (both tails)

For Left Tailed:

The critical region is in the extreme left region (left tail)

For Right Tailed:

The critical region is in the extreme right region (right tail)

Decision criterion using Critical Regions:

• If the statistic falls within the critical region we reject H_0 at a level of significance.
• If the test statistic does not fall in the critical region, we fail to reject H_0 at an alpha level.

One-Sample Z-Test Example:

import numpy as np
from scipy import stats

# Example data
heights = [68, 70, 72, 69, 65, 71, 67, 70, 74, 66, 68, 73, 69, 70, 72, 75, 71, 69, 68, 70]
population_mean = 70
population_std = 3  # Assume known population standard deviation

# Sample statistics
sample_mean = np.mean(heights)
sample_size = len(heights)

(Right-Tailed)

For the hypotheses:

# Right-Tailed Z-Test
z_score_right = (sample_mean - population_mean) / (population_std / np.sqrt(sample_size))

# Critical value for alpha = 0.05 (right-tailed)
alpha = 0.05
z_critical_right = stats.norm.ppf(1 - alpha)

print("One-Sample Z-Test (Right-Tailed):")
print("Z-score:", z_score_right)
print("Critical value:", z_critical_right)
print("Reject H0:" if z_score_right > z_critical_right else "Fail to reject H0")

# One-Sample Z-Test (Right-Tailed):
# Z-score: -0.22360679774998743
# Critical value: 1.6448536269514722
# Fail to reject H0

(Left-Tailed)

For the hypotheses:

# Left-Tailed Z-Test
z_score_left = (sample_mean - population_mean) / (population_std / np.sqrt(sample_size))

# Critical value for alpha = 0.05 (left-tailed)
z_critical_left = stats.norm.ppf(alpha)

print("One-Sample Z-Test (Left-Tailed):")
print("Z-score:", z_score_left)
print("Critical value:", z_critical_left)
print("Reject H0:" if z_score_left < z_critical_left else "Fail to reject H0")

# One-Sample Z-Test (Left-Tailed):
# Z-score: -0.22360679774998743
# Critical value: -1.6448536269514729
# Fail to reject H0

(Two-Tailed)

For the hypotheses:

# Two-Tailed Z-Test
z_score_two_tailed = (sample_mean - population_mean) / (population_std / np.sqrt(sample_size))

# Critical values for alpha = 0.05 (two-tailed)
alpha = 0.05
z_critical_two_tailed = stats.norm.ppf(1 - alpha/2)

print("One-Sample Z-Test (Two-Tailed):")
print("Z-score:", z_score_two_tailed)
print("Critical values:", -z_critical_two_tailed, "and", z_critical_two_tailed)
print("Reject H0:" if z_score_two_tailed < -z_critical_two_tailed or z_score_two_tailed > z_critical_two_tailed else "Fail to reject H0")

# One-Sample Z-Test (Two-Tailed):
# Z-score: -0.22360679774998743
# Critical values: -1.959963984540054 and 1.959963984540054
# Fail to reject H0

One-Sample T-Test Example:

import numpy as np
from scipy import stats

# Example data
heights = [68, 70, 72, 69, 65, 71, 67, 70, 74, 66, 68, 73, 69, 70, 72, 75, 71, 69, 68, 70]
population_mean = 70

# Sample statistics
sample_mean = np.mean(heights)
sample_std = np.std(heights, ddof=1)
sample_size = len(heights)

(Right-Tailed)

For the hypotheses:

# Right-Tailed T-Test
t_score_right = (sample_mean - population_mean) / (sample_std / np.sqrt(sample_size))

# Degrees of freedom
df = sample_size - 1

# Critical value for alpha = 0.05 (right-tailed)
alpha = 0.05
t_critical_right = stats.t.ppf(1 - alpha, df)

print("One-Sample T-Test (Right-Tailed):")
print("T-score:", t_score_right)
print("Critical value:", t_critical_right)
print("Reject H0:" if t_score_right > t_critical_right else "Fail to reject H0")

# One-Sample T-Test (Right-Tailed):
# T-score: -0.2620059725785
# Critical value: 1.729132811521367
# Fail to reject H0

(Left-Tailed)

For the hypotheses:

# Left-Tailed T-Test
t_score_left = (sample_mean - population_mean) / (sample_std / np.sqrt(sample_size))

# Critical value for alpha = 0.05 (left-tailed)
t_critical_left = stats.t.ppf(alpha, df)

print("One-Sample T-Test (Left-Tailed):")
print("T-score:", t_score_left)
print("Critical value:", t_critical_left)
print("Reject H0:" if t_score_left < t_critical_left else "Fail to reject H0")

# One-Sample T-Test (Left-Tailed):
# T-score: -0.2620059725785
# Critical value: -1.7291328115213678
# Fail to reject H0

(Two-Tailed)

# Two-Tailed T-Test
t_score_two_tailed = (sample_mean - population_mean) / (sample_std / np.sqrt(sample_size))

# Critical values for alpha = 0.05 (two-tailed)
t_critical_two_tailed = stats.t.ppf(1 - alpha/2, df)

print("One-Sample T-Test (Two-Tailed):")
print("T-score:", t_score_two_tailed)
print("Critical values:", -t_critical_two_tailed, "and", t_critical_two_tailed)
print("Reject H0:" if t_score_two_tailed < -t_critical_two_tailed or t_score_two_tailed > t_critical_two_tailed else "Fail to reject H0")

# One-Sample T-Test (Two-Tailed):
# T-score: -0.2620059725785
# Critical values: -2.093024054408263 and 2.093024054408263
# Fail to reject H0

Two-Sample Tests

Hypothesis testing for two samples involves comparing the means of two different groups to determine if there is a significant difference between them.

Formulating Hypotheses:

1. Null Hypothesis (H_0):

This hypothesis states that there is no significant difference between the means of the two groups, except for a specific difference.

2. Alternative Hypothesis (H_1):

Depending on the research question, the alternative hypothesis can be one of the following:

Calculate the test statistic:

1. Two-Sample Z-Test

The Z-test is used when the population variances are known and the sample sizes are large (usually N > 30).

Test statistic:

2. Two-Sample T-Test

The t-test is used when the population variances are unknown and the sample sizes are small.

Equal Variances Assumed:

Variance:

Test statistic:

Degrees of freedom:

Unequal Variances Assumed:

Test statistic:

Degrees of freedom (approximation):

Example:

Here's the Python code for both the Z-test and t-test:

import numpy as np
import scipy.stats as stats

# Data
x1, s1, n1 = 75, 10, 30
x2, s2, n2 = 70, 8, 25
d0 = 0

# Z-Test
z_score = (x1 - x2 - d0) / np.sqrt(s1**2 / n1 + s2**2 / n2)
z_critical = stats.norm.ppf(1 - 0.05 / 2)
print("Two-Sample Z-Test:")
print("Z-score:", z_score)
print("Critical values:", -z_critical, "and", z_critical)
print("Reject H0" if z_score < -z_critical or z_score > z_critical else "Fail to reject H0")

# Two-Sample Z-Test:
# Z-score: 2.0596313864290865
# Critical values: -1.959963984540054 and 1.959963984540054
# Reject H0

# Equal variances assumed

# Variance
sp2 = ((n1 - 1) * s1**2 + (n2 - 1) * s2**2) / (n1 + n2 - 2)
sp = np.sqrt(sp2)

t_score_equal = (x1 - x2 - d0) / (sp * np.sqrt(1/n1 + 1/n2))
df_equal = n1 + n2 - 2
t_critical_equal = stats.t.ppf(1 - 0.05 / 2, df_equal)

# Unequal variances assumed

t_score_unequal = (x1 - x2 - d0) / np.sqrt(s1**2 / n1 + s2**2 / n2)
df_unequal = ((s1**2 / n1 + s2**2 / n2)**2) / (((s1**2 / n1)**2 / (n1 - 1)) + ((s2**2 / n2)**2 / (n2 - 1)))
t_critical_unequal = stats.t.ppf(1 - 0.05 / 2, df_unequal)

print("\nTwo-Sample T-Test (Equal Variances Assumed):")
print("T-score:", t_score_equal)
print("Critical values:", -t_critical_equal, "and", t_critical_equal)
print("Reject H0" if t_score_equal < -t_critical_equal or t_score_equal > t_critical_equal else "Fail to reject H0")

# Two-Sample T-Test (Equal Variances Assumed):
# T-score: 2.018187246178143
# Critical values: -2.0057459935369497 and 2.0057459935369497
# Reject H0

print("\nTwo-Sample T-Test (Unequal Variances Assumed):")
print("T-score:", t_score_unequal)
print("Critical values:", -t_critical_unequal, "and", t_critical_unequal)
print("Reject H0" if t_score_unequal < -t_critical_unequal or t_score_unequal > t_critical_unequal else "Fail to reject H0")

# Two-Sample T-Test (Unequal Variances Assumed):
# T-score: 2.0596313864290865
# Critical values: -2.0058102585878848 and 2.0058102585878848
# Reject H0

Paired T-Test

The paired t-test is used to determine whether the mean difference between paired observations is significantly different from zero. Paired observations often arise in before-and-after studies, matched subjects, or cases where measurements are taken under two different conditions on the same subjects.

Formulating Hypotheses:

1. Null Hypothesis (H_0):

This hypothesis states that the mean difference between the paired observations is zero.

2. Alternative Hypothesis (H_1):

(H_1) can be:

Test Statistic:

The test statistic for a paired t-test is calculated as follows:

Degrees of Freedom:

df = n - 1

Example:

Suppose we have the following data from a study comparing the test scores of students before and after a training program:

import numpy as np
import scipy.stats as stats

# Data
before = np.array([80, 78, 90, 84, 76])
after = np.array([85, 82, 91, 86, 80])

# Calculate differences
differences = after - before
mean_diff = np.mean(differences)
std_diff = np.std(differences, ddof=1)
n = len(differences)

# Calculate t statistic
t_stat = mean_diff / (std_diff / np.sqrt(n))

# Degrees of freedom
df = n - 1

# Critical value for two-tailed test at alpha = 0.05
t_critical = stats.t.ppf(1 - 0.05 / 2, df)

print("Paired T-Test:")
print("Mean difference:", mean_diff)
print("Standard deviation of differences:", std_diff)
print("T-statistic:", t_stat)
print("Critical value:", t_critical)
print("Reject H0" if abs(t_stat) > t_critical else "Fail to reject H0")

# Paired T-Test:
# Mean difference: 3.2
# Standard deviation of differences: 1.6431676725154984
# T-statistic: 4.354648431614539
# Critical value: 2.7764451051977987
# Reject H0

One-Way ANOVA Test / F-Test

One-Way ANOVA (Analysis of Variance) and the F-test are statistical techniques used to compare means among groups and determine if there are any statistically significant differences between them. One-Way ANOVA is particularly useful when comparing three or more groups, while the F-test is often used in the context of One-Way ANOVA to test the null hypothesis that the means of different groups are equal.

Formulating Hypotheses:

1. Null Hypothesis (H_0):

All group means are equal.

2. Alternative Hypothesis (H_1):

At least one group mean is different.

Test Statistic:

The test statistic for a F-test is calculated as follows:

Here,

It measures the variation within the groups.

It measures the variation between the group means and the overall mean.

It measures the total variation in the data.

K is the number of groups or treatments.

N is the total number of observations across all groups.

Critical Value:

import numpy as np
import scipy.stats as stats

# Sample data
group1 = [85, 88, 90, 92, 85]
group2 = [78, 80, 82, 84, 85]
group3 = [92, 85, 88, 91, 89]

# Perform One-Way ANOVA
f_stat, p_value = stats.f_oneway(group1, group2, group3)

# Calculate degrees of freedom
k = 3  # number of groups
n = len(group1) + len(group2) + len(group3)  # total number of observations
df_between = k - 1
df_within = n - k

# Significance level
alpha = 0.05

# F-critical value
f_critical = stats.f.ppf(1 - alpha, df_between, df_within)

print(f"F-statistic: {f_stat}")
print(f"F-critical value: {f_critical}")

# Interpretation
if f_stat > f_critical:
    print("Reject the null hypothesis: There is a significant difference between the group means.")
else:
    print("Fail to reject the null hypothesis: There is no significant difference between the group means.")

# F-statistic: 9.05555555555555
# F-critical value: 3.8852938346523933
# Reject the null hypothesis: There is a significant difference between the group means.