Hashing in C++

What is Hashing?

Hashing is a technique or process of mapping keys/data into the hash table by using a hash function. It is done for faster access to elements.

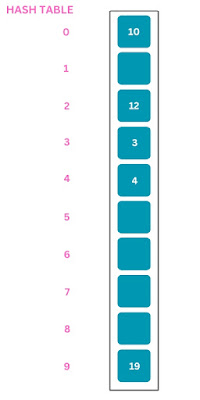
Let a hash function H(k) maps the value k at the index k mod 10 in an array.

Keys/Data = [12, 19, 10, 3, 4]

Find hash value of key using hash function:

k = 12

H(12) = 12 mod 10 = 2

k = 19

H(19) = 19 mod 10 = 9

k = 10

H(10) = 10 mod 10 = 0

k = 3

H(3) = 3 mod 10 = 3

k = 4

H(4) = 4 mod 10 = 4

Problem with Hashing

What if there is another value 22 then hash key of 22 will be 2 and index 2 is already occupied. This is known as collision and it creates problem in searching, insertion, deletion, and updating of value.

Collision resolution in Hashing:

1. Separate Chaining (Open Hashing)

2. Open Addressing (Closed Hashing):

• Linear Probing
• Quadratic Probing
• Double Hashing

Separate Chaining:

Make each cell of the hash table point to an array/vector of records that have the same hash function value.

#include <iostream>
#include <list>
#include <vector>
using namespace std;

// HashTable class using separate chaining
class HashTable {
private:
    int tableSize; // Size of the hash table
    vector<list<int>> table; // Vector of lists for separate chaining

    // Hash function to map values to key
    int hashFunction(int key) {
        return key % tableSize;
    }

public:
    // Constructor to initialize the hash table
    HashTable(int size) {
        tableSize = size;
        table.resize(tableSize);
    }

    // Function to insert a key into the hash table
    void insert(int key) {
        int index = hashFunction(key); // Get the index for the key
        table[index].push_back(key); // Insert the key into the appropriate list
    }

    // Function to remove a key from the hash table
    void remove(int key) {
        int index = hashFunction(key); // Get the index for the key

        // Traverse the list to find the key and remove it
        for (auto it = table[index].begin(); it != table[index].end(); ++it) {
            if (*it == key) {
                table[index].erase(it);
                return;
            }
        }

        cout << "Key " << key << " not found!" << endl; // Key not found
    }

    // Function to search for a key in the hash table
    bool search(int key) {
        int index = hashFunction(key); // Get the index for the key

        // Traverse the list to find the key
        for (auto it = table[index].begin(); it != table[index].end(); ++it) {
            if (*it == key) {
                return true; // Key found
            }
        }

        return false; // Key not found
    }

    // Function to display the contents of the hash table
    void displayHashTable() {
        for (int i = 0; i < tableSize; ++i) {
            cout << "Index " << i << ":";
            for (auto x : table[i]) {
                cout << " --> " << x;
            }
            cout << endl;
        }
    }
};

// Main function to demonstrate the HashTable class
int main() {
    // Create a hash table of size 10
    HashTable ht(10);

    // Insert keys into the hash table
    ht.insert(10);
    ht.insert(20);
    ht.insert(30);
    ht.insert(40);
    ht.insert(50);
    ht.insert(15);
    ht.insert(25);
    ht.insert(35);

    // Display the hash table
    cout << "Hash Table contents:" << endl;
    ht.displayHashTable();
    // Expected Output:
    // Index 0: --> 10 --> 20 --> 30 --> 40 --> 50
    // Index 1:
    // Index 2:
    // Index 3:
    // Index 4:
    // Index 5: --> 15 --> 25 --> 35
    // Index 6:
    // Index 7: 
    // Index 8:
    // Index 9:

    // Search for keys in the hash table
    cout << "Search for key 20: " << (ht.search(20) ? "Found" : "Not Found") << endl;
    // Output: Search for key 20: Found
    cout << "Search for key 45: " << (ht.search(45) ? "Found" : "Not Found") << endl;
    // Output: Search for key 45: Not Found

    // Remove keys from the hash table
    ht.remove(20);
    ht.remove(35);
    ht.remove(45); // Key not in the hash table

    // Display the hash table after removal
    cout << "Hash Table contents after removal:" << endl;
    ht.displayHashTable();
    // Expected Output:
    // Index 0: --> 10 --> 30 --> 40 --> 50
    // Index 1:
    // Index 2:
    // Index 3:
    // Index 4:
    // Index 5: --> 15 --> 25
    // Index 6:
    // Index 7: 
    // Index 8:
    // Index 9:

    return 0;
}

Open Addressing:

Linear Probing

In linear probing, the hash table is searched sequentially that starts from original location of the hash. If incase the location that we get is already occupied, then we check for the next location.

Algorithm:

1. Calculate the hash key i.e. key = data % size
2. Check if hashTable[key] is empty. Store the value directly by hashTable[key] = data
3. If the hash index already has some value, then check for the next index using: key = (key + 1) % size
4. Check if the next index is available hashTable[key] then store the value. Otherwise try for next index.
5. Do the above process till we find the space.

For example:

H(k) = k mod 6

Keys/Data = [3, 5, 15]

If collision exists, use the following hash function:

H`(k) = (H(k) + i) mod 6         where i = number of attempt

Quadratic Probing:

Quadratic probing operates by taking the original hash index and adding successive value of an arbitrary quadratic polynomial until an open slot is found.

If collision exists:

H`(k) = (H(k) + (i^2)) mod size

Double Hashing:

In double hashing, If collision exists:

H`(k) = (H(k) + i * (H``(k))) mod size

where H``(k) = size - (k mod size)

#include<iostream>
using namespace std;

class HashItem
{
    int Key;    // The key for the hash item
    int Value;  // The value associated with the key
    int Status; // 0: Empty, 1: Deleted, 2: Occupied

    // Allow HashTable class to access private members of HashItem
    friend class HashTable;
};

class HashTable
{
private:
    HashItem* HashArray; // Dynamic array to hold hash items
    int Capacity;        // Capacity of the hash table
    int currentElements; // Current number of elements in the hash table

    // Function to get the next index using linear probing
    int getNextCandidateIndex(int key, int i)
    {
        return (key + i) % Capacity;
    }

    // Function to double the capacity of the hash table
    void doubleCapacity()
    {
        int oldCapacity = Capacity;
        HashItem* oldHashArray = HashArray;

        // Double the capacity
        Capacity *= 2;
        HashArray = new HashItem[Capacity];

        // Initialize new hash array
        for (int i = 0; i < Capacity; i++)
            HashArray[i].Status = 0;

        // Rehash all elements from old hash array to new hash array
        for (int i = 0; i < oldCapacity; i++)
        {
            if (oldHashArray[i].Status == 2)
            {
                int key = oldHashArray[i].Key;
                int index = getNextCandidateIndex(key, 0);

                int j = 1;
                while (HashArray[index].Status == 2)
                {
                    index = getNextCandidateIndex(key, j);
                    j++;
                }

                HashArray[index].Key = key;
                HashArray[index].Value = oldHashArray[i].Value;
                HashArray[index].Status = 2;
            }
        }

        // Delete old hash array
        delete[] oldHashArray;
    }

public:
    // Constructor to initialize hash table with default capacity
    HashTable()
    {
        Capacity = 10;
        HashArray = new HashItem[Capacity];
        currentElements = 0;

        for (int i = 0; i < Capacity; i++)
            HashArray[i].Status = 0;
    }

    // Constructor to initialize hash table with given capacity
    HashTable(int capacity)
    {
        Capacity = capacity;
        HashArray = new HashItem[Capacity];
        currentElements = 0;

        for (int i = 0; i < Capacity; i++)
            HashArray[i].Status = 0;
    }

    // Destructor to free allocated memory
    ~HashTable()
    {
        delete[] HashArray;
    }

    // Function to insert a key-value pair into the hash table
    void insert(int key, int value)
    {
        int index = getNextCandidateIndex(key, 0);

        int i = 1;
        // Find an empty or deleted spot using linear probing
        while (HashArray[index].Status == 2)
        {
            index = getNextCandidateIndex(key, i);
            i++;
        }

        // Insert the key-value pair
        HashArray[index].Key = key;
        HashArray[index].Value = value;
        HashArray[index].Status = 2;
        currentElements++;

        // If the load factor is 0.75 or more, double the capacity
        if (currentElements >= 0.75 * Capacity)
            doubleCapacity();
    }

    // Function to delete a key from the hash table
    bool deleteKey(int key)
    {
        int index = getNextCandidateIndex(key, 0);

        int i = 1;
        // Find the key using linear probing
        while (HashArray[index].Status != 0 && HashArray[index].Key != key)
        {
            index = getNextCandidateIndex(key, i);
            i++;
        }

        // If key is found, mark it as deleted
        if (HashArray[index].Status == 2 && HashArray[index].Key == key)
        {
            HashArray[index].Status = 1;
            currentElements--;
            return true;
        }

        // Key not found
        return false;
    }
};

int main()
{
    HashTable hashtable(6);

    hashtable.insert(3, 1);
    hashtable.insert(5, 2);
    hashtable.insert(15, 3);

    return 0;
}